leakdetection-technology.com

Laminar Flow

Laminar flow is defined as a parallel flow of molcules in a pipe, whereby the transverse distribution of the speed of the molecules is parabolic.

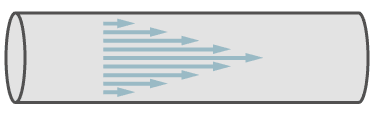
Path of molecules in laminar flow.

In the figure, the arrows symbolise the speed of the molecules. In the center of the pipe the speed is a maximum and it decreases towards the walls of the pipe.

The most wellknown formula for laminar flow is from Poisseuille. It describes the laminar flow through a straight tubulation with circular cross-section.

$q = \frac{\pi \cdot r^4}{16 \cdot \eta \cdot l} \, ({p_1}^2 - {p_2}^2)$

$\eta = \textup {dynamic viscosity of the gas [bar x s]}$

$l = \textup {length of the round tube (capillary)}$

$r = \textup {radius of the capillary }$

$p_1 = \textup {the higher pressure }$

$p_2 = \textup {the lower pressure}$

$q = \textup {pressure x volume / time (leak rate)}$

If one assumes that the geometry dimensions of a leak do not change during the period of measurement, the constants of the Poiseuille formula can be combined in one constant K:

$q = K \, \frac {({p_1}^2-{p_2}^2)}{\eta}$

Where K contains the following constants:

$K = \, \frac {\pi \cdot r^4}{16 \cdot l}$

We can now see from this formula some properties of laminar flow: When the pressure difference across a leak changes, the leakrate changes with the square of the pressure according to the following formula:

$\frac{q_A}{({p_{A1}}^2-{p_{A2}}^2)} = \frac{q_B}{({p_{B1}}^2-{p_{B2}}^2)}$

From this we conclude that with increasing pressure in an object under leaktest a drastic increase of sensitivity can be achieved. On large containers which are filled with a search gas (for example Helium) to make a sniffer-test, a cost reduction can be achieved by increasing the inner total pressure, but reducing the concentration of the test gas. Of course the safety conditions for filling containers with pressurised gas must be followed.