leakdetection-technology.com

Molecular Flow

Molecular flow exists in small leaks and at low pressures. At molecular flow each molecule travels independently of other molecules. The mean free path is larger than the diameter of the leak capillary. Therefore it is possible, that a single molecule travels against the general flow direction, because molecules do not collide with each other, but only with the walls. Despite this fact, the general flow is in direction of the lower pressure. At molecular flow the molecules follow the partial pressure down gradient.

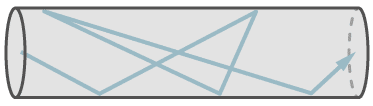
The figure shows the flow of a single molecule through a leak at molecular flow.

The formula of Knudsen for the leak rate at molecular flow is:

$q=\frac {\sqrt{2\pi}}{ 6 } \sqrt { \frac { R\cdot T }{ M } } \frac { { d }^{ 3 } }{ l } \left( { p }_{ 1 }-{ p }_{ 2 } \right)$

$\textup {R = universal gasconstant}$

$\textup {T = absolute temperature (K)}$

$\textup {M = relative mass of molecule}$

$\textup {p1 = the higher pressure}$

$\textup {p2 = the lower pressure}$

$\textup {d = diameter of the leak}$

$\textup {l = length of the leak}$

From the Knudsen´s formula one can see that contrary to the laminar flow, the leakrate follows linear proportion to pressure difference. To calculate a leakrate after a pressure change, the following formula is valid:

$\frac{q_A}{(p_{A1} - p_{A2})} = \frac{q_B}{(p_{B1} - p_{B2})}$

The dependency of the leakrate on molecular flow in relation to the type of gas, follows inverse proportion to the square root of the relative mass of molecules. Contrary to the laminar flow, a change of gas can make larger differences in leakrate (at constant pressure difference), as shown in the next formula:

$\frac{q_A}{q_B} = \frac{\sqrt{M_B}}{\sqrt{M_A}}$